For the matlab code in this post I used the java brush, therefore the comments will need to be changed from // to %. I know you would ask, why I didn't use a Matlab brush in the first place, well I am using the SyntaxHighlighter and looking at this comment "Note from author: the long list of functions (1300) can make the browser unresponsive when you use this brush."put me off.
I Black-Scholes equation
The black-Scholes equation \[\frac{\delta V}{\delta t}+\frac{1}{2}\sigma^2 S^2 \frac{\delta^2 V}{\delta S^2}+r S \frac{\delta V}{\delta S} - r V = 0 \]
Where $S=\mbox{Stock price},\sigma=Volatility,r=\mbox{Interest Rate},V=\mbox{Option Value}$This is a linear parabolic equation partial differential equation.
In terms of Greeks, the Black-Scholes equation can be written as follow \[ \Theta = -\frac{1}{2} \sigma^2 S^2 \Gamma - r S \Delta + r V\]
Final & Boundary Conidions
- Final condition is the Payoff
- Boundary conditions at $S=0\$ and at $S=\infty\$
European Call Option
- Payoff $C_{E}(S,T) = max(S-E,0)\$
- Boundary Conditions :
- At $S=0 \qquad V(S,T) = 0\$
- At $S=\infty \qquad V(S,T) = S\$
Black-Scholes closed from solution
The closed form solution for the Black-Scholes equation for a European Call option is
\[C(S,T) = S\quad N(d_1) - E\quad e^{-r(T-t)}\quad N(d_2)\]
where \[d_1 = \frac{log(\frac{S}{E}) + (r+\frac{1}{2}\sigma^2)(T-t)}{ \sigma \sqrt{T-t}}\],
\[d_2 = \frac{log(\frac{S}{E}) + (r-\frac{1}{2}\sigma^2)(T-t)}{ \sigma \sqrt{T-t}}\]
and $N\$ is the cumulative distribution function of a standard normal.
Using the Call-Put parity equation $CALL-PUT = S - e^{-r (T-t)} N(-d_2)\$ we can also rite the put formula \[P(S,T) = -S\quad N(-d_1) + E\quad e^{-r(T-t)}\quad N(-d_2)\]
For Binary type options, also called cash-or-nothing the Call and Put values:
\[C_B(S,T) =e^{-r(T-t)}\quad N(d_2)\]
\[P_B(S,T)=e^{-r(T-t)}\quad (1-N(d_2))\]
II Finite Difference Method
Finite difference method is a numerical methods for approximating the solutions to differential equations using finite difference equation to approximate derivative.
The finite-difference grid usually has equal time step, the time between nodes is equal S steps.
The time step is $\delta t\$ and the asset step is $\delta S\$. Thus the grid is made up of points at asset Values $S=i\delta S\$ and times $t= T-k \delta t\$ where $0\leq i\leq l \$ and $0\leq k\leq K \$.
$ I \delta S\$ is our approximation of infinity, in this exercise we will use $S_\infty = 2 \cdot Strike\$
Thus we can write the option value at each of these grid point as \[V^{k}_{i}=V(i\delta S, T-k\delta t)\]
So that the superscript is the time variable and the subscript is the asset variable.
Now we will use the Black-Scholes Greeks notation to approximate theta, gamma and delta
Approximating $\Theta\$
The definition of the first derivative of V is \[\frac{\delta V}{\delta t} = \lim\limits_{\delta t \to 0} \frac{V(S,t+\delta t) - V(S,t)}{\delta t} \]
It follows that we can approximate the time derivative from our grid of values using the backward difference of time: \[\frac{\delta V}{\delta t}(S,t) \approx \frac{V^{k}_{i}-V^{k+1}_{i}}{\delta t} + O(\delta t) \]
This is the approximation of the option's theta. It uses the option value at two points of the grid V(k,i) and V(k+1,i). This approximation is one order accurate in delta t and we will see later that later in the examples.
Approximating $\Delta\$
The same idea can be used to approximate the first order in S derivative, the delta. From a Taylor series expansion of the option value about the point $S+\delta S,t\$ we have \[V(S+\delta S,t)=V(S,t) + \delta S \frac{\delta V}{\delta S}(S,t) + \frac{1}{2}\delta S^2 \frac{\delta^2 V}{\delta S^2}(S,t)+O(\delta S^3)\]
Similarly, \[V(S-\delta S,t)=V(S,t) - \delta S \frac{\delta V}{\delta S}(S,t) + \frac{1}{2}\delta S^2 \frac{\delta^2 V}{\delta S^2}(S,t)-O(\delta S^3)\] Subtracting from the other, dividing by $ 2\delta S\$ and rearranging gives \[\frac{\delta V}{\delta S}(S,t) = \frac{V^{k}_{i+1}-V^{k}_{i-1}}{2\delta S}+O(\delta S^2)\]
Approximating $\Gamma\$
The gamma of an option is the second derivative of the option with respect to the underlying, The natural approximation is \[\frac{\delta^2 V}{\delta S^2}\approx \frac{V^{k}_{i+1}-2V^{k}_{1}+V^{k}_{i-1}}{\delta S^2} + O(\delta S^2)\] This approximation is also a second order accurate in $\delta S\$ as the approximation the $\Delta\$ and will show this also later.
The Explicit Finite-Diffrence Method
Calculation of the Greeks using the backward difference
Now we plug our previous Greeks approximation into the Black-Scholes equation \[\frac{V^{k}_{i}-V^{k-1}_{i}}{\delta t}+\frac{1}{2}\sigma^2(i^2\delta S^2) [\frac{V^{k}_{i-1}-2V^{k}_{i}+V^{k}_{i+1}}{\delta S^2}] +r i\delta S [\frac{V^{k}_{i+1}-V^{k}_{i-1}}{2\delta S}]- r V^{k}_{i}=0\] Rearranging \[V^{k-1}_{i}= \alpha_{i} V^{k}_{i-1} + \beta_{i} V^{k}_{i} + \gamma_{i} V^{k}_{i+1}\] with \[\alpha_{i} = \frac{1}{2}\sigma^2 i^2 \delta t - \frac{1}{2} i r \delta t\] \[\beta_{i}= 1 - \sigma^2 i^2 \delta t - r \delta t\] \[\gamma_{i}=\frac{1}{2}\sigma^2 i^2 \delta t + \frac{1}{2} i r \delta t\]
The finite difference equation is valid everywhere inside the grid that is not valid on the boundaries. Therefore we need to define the boundaries depending on the option type we are valuing.
The finite difference equation is valid everywhere inside the grid that is not valid on the boundaries. Therefore we need to define the boundaries depending on the option type we are valuing.
Final & Boundary conditions
For a European Call opation at t = T(expiry); i = I \[Payoff V(S,t) = max(S-E,0)\] Thus \[V^{k}_{i} = max(i \delta S-E, 0) \] where $ 0\leq i \leq l \$
At S = 0
The Black-Scholes equation become \[\frac{\delta V}{\delta t}=r V \to V^{k}_{i}-V^{k-1}_{i}=r V^{k}_{i}\delta t\] But at $S=0,i =0,V^{k}_{0}-V^{k-1}_{0}=rV^{k}_{0}\delta t\$ Thus $V^{k-1}_{0}=(1-r\delta t)V^{k}_{0}\$
At $t=\infty\$
The probability of S falling under E becomes negligible, also small changes in S fo not affecto the option price, then $\Gamma=\frac{\delta \Delta}{\delta S}=0\$ (For European Call option) \[\Gamma\approx\frac{V^{k}_{i-1}-2V^{k}_{i}+V^{k}_{i+1}}{\delta S^2}=0\]
At i = I
This is the upper boundary condition \[V^{k-1}_{i}=(\alpha_{I}-\gamma_{I})V^{k}_{I-1}+(\beta_{I}+2\gamma_{I})V^{k}_{I})\] Finally for the stability criteria we will choose $\delta t \leq \frac{1}{I\sigma^2}\$.
III Code and Results
Here is the matlab implementation of the finite difference method. We used the same fixed parameters i.e volatility =0.2, Interest Rate =0.05, Strike Price = 100, current price is the discounted value of the strike price $S=100 e^{-rT}/$.
For each type of option we vary the time step and the asset price to show that the method is first order and second order accurate in $\delta t\$ and $\delta S\$ in turn.
We also defnie the $\alpha,\beta and \gamma\$ externally for clarity.
The $\alpha\$ function code
function [ alpha ] = alphaN( n, sigma, r,dt )
//ALPHAN return the alhpa value
//for Finite Difference Method
//From the Black-Sholes FDM equation
//Alpha =0.5*(sigma^2)*(n^2)*dt-0.5*n*r*dt;
alpha = 0.5 * (sigma^2) * (n^2) * dt - 0.5 * n * r * dt;
end
The $\beta\$ function code
function [ beta ] = betaN( n, sigma, r,dt ) //BETAN return the beta value for Finite Difference Method //From the Black-Sholes FDM equation //betaN = beta = 1 - (sigma^2) * (n^2) * dt - r * dt; beta = 1 - (sigma^2) * (n^2) * dt - r * dt; end
The $\Gamma\$ function code
function [ gamma ] = gammaN( n, sigma, r,dt ) //GAMMAN return the gamma value for Finite Difference Method //From the Black-Sholes FDM equation //gamma = 0.5 * (sigma^2) * (n^2) * dt + 0.5 * n * r * dt; gamma = 0.5 * (sigma^2) * (n^2) * dt + 0.5 * n * r * dt; end
We have also defnied the results for the closed form solution for a European Call and put option and similarly for the binary options.
Closed form solution for European Call option
function [ val ] = BS_CALL( S, E , r , sigma ,T , t ) //BS_CALL Closed form solution using the Black-Scholes //equation to price a european CALL option d1 = (log( S/E) + ( r + 0.5 * sigma^2) * (T-t))/(sigma * sqrt(T-t)); d2 = d1-sqrt(T-t)*sigma; val = S * normcdf(d1) - E* exp(-r *(T-t)) * normcdf(d2); end
Closed form solution for European Put option
function [ val ] = BS_PUT( S, E , r , sigma ,T , t ) //BS_PUT Closed form solution using the Black-Scholes //equation to price a european PUT option d1 = (log( S/E) + ( r + 0.5 * sigma^2) * (T-t))/(sigma * sqrt(T-t)); d2 = d1-sqrt(T-t)*sigma; val = -S * normcdf( - d1) + E * exp( -r * (T-t) ) * normcdf( - d2 ); end
Closed form solution for a European Call option (Cash-or-nothing)
function [ val ] = BS_CALL_B( S, E , r , sigma ,T , t ) //BS_CALL_B Closed form solution using the Black-Scholes //equation to price a european CALL option for a Cash or nothing option d1 = (log( S/E) + ( r + 0.5 * sigma^2) * (T-t))/(sigma * sqrt(T-t)); d2 = d1-sqrt(T-t)*sigma; val = exp( -r * (T-t) ) * normcdf(d2); endClosed form solution for a European Put option (Cash-or-nothing)
function [ val ] = BS_PUT_B( S, E , r , sigma ,T , t ) //BS_PUT_B Closed form solution using the Black-Scholes //equation to price a european CALL option for a Cash or nothing option d1 = (log( S/E) + ( r + 0.5 * sigma^2) * (T-t))/(sigma * sqrt(T-t)); d2 = d1-sqrt(T-t)*sigma; val = exp( -r * (T-t) ) * (1- normcdf(d2)); endHere we define the option value function for a European Call and put option with respective payoff condition max(S-E,0) and mad(E-S,0). we notice that the code is similar only the payoff function can be reversed depending on the option type i.e call or a put.
Option Value Function
function [ Err_perc dt ds ] = Option_Value( S,vol, Int_Rate, PType, Strike, Expiration, NAS )
//OPTION_VALUE
// vol : volatility
// Int_Rate : Interest Rate
// Option Type: Put/Call
// Strike : Strike price
// Expiration : Experiy date
// NAS : number os asset steps
ds = 2 * Strike / NAS; //Infinity is defined as twise the strike price
dt = 0.9 / (vol^2 * NAS^2) ;//For stability
NTS = round( Expiration / dt ) + 1; //Number of time steps
dt = Expiration / NTS; // to ensure the expiration is an integer number of time steps
v = zeros(NAS, NTS); //option price grid
q = 1;
if ( strcmp(PType , 'PUT'))
q = -1 ;
end
//Define boundary condition at expiriy
temp = (0:NAS-1);
V( :,NTS) = max( q * ( temp * ds - Strike) , 0);
%at S = 0;
%V(m-1, 0) = (1 - r dt) * V(m,0)
for i = NTS : -1 : 2
V(1,i-1) = ( 1 - Int_Rate * dt) * V(1, i);
end
for j = NTS : -1: 2
for i = 2: NAS -1
V(i,j-1) = alphaN(i,vol,Int_Rate,dt) * V(i-1,j) +
betaN(i,vol,Int_Rate,dt) * V(i,j) +
gammaN(i,vol,Int_Rate,dt) * V(i+1,j);
end
//Satisfy boundary conditions
V(NAS,j-1) = (alphaN(i,vol,Int_Rate,dt) -
gammaN(i,vol,Int_Rate,dt) ) * V(NAS-1,j) +
( betaN(i,vol,Int_Rate,dt) +
2* gammaN(i,vol,Int_Rate,dt) ) * V(NAS,j);
end
cFormSolution = 0;
if ( strcmp(PType , 'CALL'))
cFormSolution = BS_CALL( S, Strike , Int_Rate , vol ,Expiration , 0)
else
cFormSolution = BS_PUT( S, Strike , Int_Rate , vol ,Expiration , 0)
end
//pick up the option price at t = 0
index = round((S/ds)+1)
//Error with the closed form solution
Err = cFormSolution - V(index,1);
//Error with the closed form solution in percentage
Err_perc = abs( Err/cFormSolution )
end
Binary option value function
function [ Err_perc dt ds ] = Option_Value_B( S,vol, Int_Rate, PType, Strike, Expiration, NAS )
//OPTION_VALUE
// vol : volatility
// Int_Rate : Interest Rate
// Option Type: Put/Call
// Strike : Strike price
// Expiration : Experiy date
// NAS : number os asset steps
ds = 2 * Strike / NAS; //Infinity is defined as twise the strike price
dt = 0.9 / (vol^2 * NAS^2) ;%For stability
NTS = round( Expiration / dt ) + 1 //Number of time steps
dt = Expiration / NTS; // to ensure the expiration is an integer number of time steps
v = zeros(NAS, NTS);
q = 1;
if ( strcmp(PType , 'PUT'))
q = -1 ;
end
for i = 1 : NAS
if( max( q * ( i * ds - Strike) , 0) >= 0 )
V(i,NTS) = 1;
else
V(i,NTS) = 0;
end
end
//at S = 0;
//V(m-1, 0) = (1 - r dt) * V(m,0)
for i = NTS : -1 : 2
V(1,i-1) = ( 1 - Int_Rate * dt) * V(1, i);
end
for j = NTS : -1: 2
for i = 2: NAS -1
V(i,j-1) = alphaN(i,vol,Int_Rate,dt) * V(i-1,j) + betaN(i,vol,Int_Rate,dt) * V(i,j) + gammaN(i,vol,Int_Rate,dt) * V(i+1,j);
end
%Satisfy boundary conditions
V(NAS,j-1) = (alphaN(i,vol,Int_Rate,dt) - gammaN(i,vol,Int_Rate,dt) ) * V(NAS-1,j) + ( betaN(i,vol,Int_Rate,dt) + 2* gammaN(i,vol,Int_Rate,dt) ) * V(NAS,j);
end
cFormSolution = 0;
if ( strcmp(PType , 'CALL'))
cFormSolution = BS_CALL_B( S, Strike , Int_Rate , vol ,Expiration , 0)
else
cFormSolution = BS_PUT_B( S, Strike , Int_Rate , vol ,Expiration , 0)
end
index = round((S/ds)+1)
Err = cFormSolution - V(index,1);
Err_perc = abs( Err/cFormSolution )
end
In the figure below we output the call option values by the explicit finite-difference method.
In the following we will show that the finite-difference methods is first order and second order accurate in $\delta t\$ and $\delta S\$ in turn by plotting the Error against $\delta t\$ and $\delta S^2\$ in both plot we expect to have a linear plot.
European Call option values Error Vs. $\delta t\$

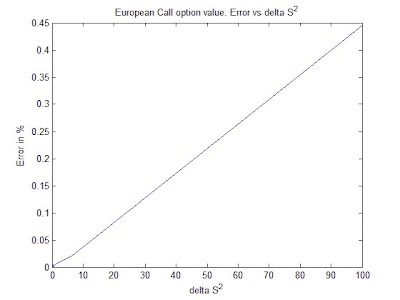
European Call option values Error Vs. $\delta S^2\$
European Put option values Error Vs. $\delta t\$

European Put Option values error Vs. $\delta S^2\$

Plotting the error in percentage against the $\delta t\$ and $\delta S^2\$ for the European call and put option for both payoff function continuous and binary, we clearly see that the error is linear in $\delta t\$ and $\delta S^2\$.
The smaller the steps are in $\delta t\$ and $\delta S^2\$ the precise the finite-difference method is but this come with an expensive computation time.
References
Paul Wilmott Introduces Quantitative Finance, Second Edition, by Paul P.Wilmott
Options, Futures, and Other Derivatives (Prentice Hall Series in Finance), Seventh Edition, by John C.Hull


6 comments:
These scams may possibly involve credit refusals, payment issues, software manipulation along with identity theft. Binary Trading Options A ring of brokers who had been using software to promise "losers" was recently indicted.
7 steps to health & the big diabetes lie is an excellent program, which is especially designed for the diabetes people who are all suffering in a long run in diabetes & 7 steps to health And The Big Diabetes Lie helps how to control your blood sugar level. 7 steps to health And The Big Diabetes Lie is a total natural home course which doesn’t require medication otherwise expensive equipment. Following properly tips and techniques included in 7 steps to health And The Big Diabetes Lie program will give you an important opportunity to be healthy pro the relax of your life. 7 steps to health And The Big Diabetes Lie program show Product Reviews some top secret on how to enhance the insulin level through natural methods, healthy meals & simple exercises.
Get the latest FOX technology news today: breaking news and analysis on computing, the web, blogs, games, gadgets, social media, broadband and more.
We are best and trusted bangladeshi online news portal website. Everyday we publish the national and international latest news. If you want to get regular newslatter from our newspaper, please go home page ক্রিকেট and click the below subscribe button.
View entertainment news and videos for the latest movie, music, TV and celebrity headlines on entertainment news for today
We are the world best leading online newspaper portal. You all are the most welcome in our newspaper.If you want to get regular newslatter from our newspaper, please go home page health news and click the below subscribe button.
World News :
View CNN world news reuters today for international news and videos from Europe, Asia, Africa, the Middle East and the Americas. Visit CNN News for up-to-the-minute news, breaking news, video, audio and feature stories.
Business News :
The latest CNN Business News: breaking personal finance, company, View the latest business news nba about the world's top companies, and explore articles on global.
Sports News :
Latest sports news football from around the world with in-depth analysis, features, photos and videos covering football, tennis, motorsport, golf, rugby, sailing, skiing, horse racing and equestrian.
Entertainment News :
View entertainment news of today and videos for the latest movie, music, TV and celebrity headlines on usacnnnews.com
Technology News :
Get the latest CNN technology news science : breaking news and analysis on computing, the web, blogs, games, gadgets, social media, broadband and more.
Science News :
Get the latest CNN Science and Environment News: breaking news, analysis and debate on science news for today and nature in the UK and around the world.
Health News :
Get the latest CNN health news recent : breaking health and medical news from the UK and around the world, with in-depth features on well-being and lifestyle.
Daily Life :
What You Need To Know About The Good Life? Get the latest lifestyle news with articles and videos on pets, parenting, fashion, beauty, food, travel, relationships and more on CNN daily life news.
Post a Comment